Calculer la racine carrée d'un nombre

Le calculateur calcule automatiquement la racine carrée du nombre indiquée. La notation est √. Par exemple la notation pour racine carrée de 9 est √9.

Qu'est ce qu'une racine carrée?

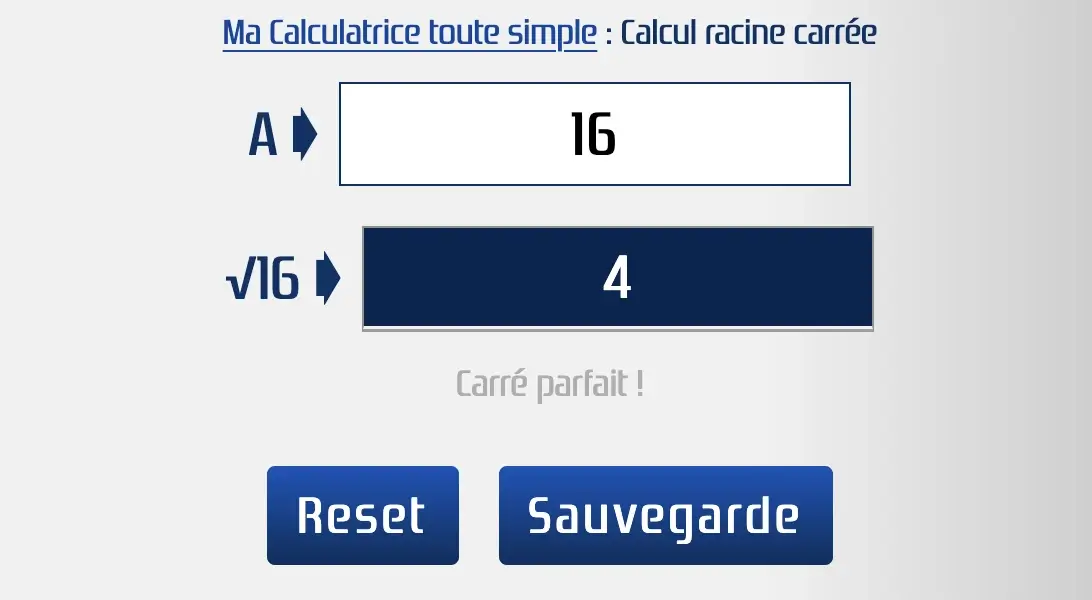
La racine carrée d'un nombre 'x' correspond au nombre 'y' qui pourra être multiplié par lui-même et qui résultera du nombre 'x'. Par exemple √9 = 3 car 3 * 3 = 3² = 9. Plus généralement si √x = y alors y² = x.

Nombre négatif

Le radicande ('x' dans √x) peut être un nombre positif ou négatif. Pour les nombres négatifs, le résultat est exprimé sous forme de nombre complexe avec l'unité imaginaire 'i'.

Nombres complexes et unité imaginaire

Lorsque vous calculez la racine carrée d'un nombre négatif, le résultat utilise l'unité imaginaire 'i' où i = √(-1). Par exemple :

• √(-4) = 2i (car √4 × √(-1) = 2 × i = 2i)
• √(-9) = 3i (car √9 × √(-1) = 3 × i = 3i)
• √(-16) = 4i (car √16 × √(-1) = 4 × i = 4i)

Cette notation est standard en mathématiques et permet de représenter les racines de nombres négatifs.

Exemple d'utilisation

Par exemple pour calculer la racine carrée de 16, indiquez 16 dans la case correspondante et le résultat apparaîtra.

Raccourcis clavier pour la racine carée

m ⇝ Effacer

f ⇝ Sauvegarder

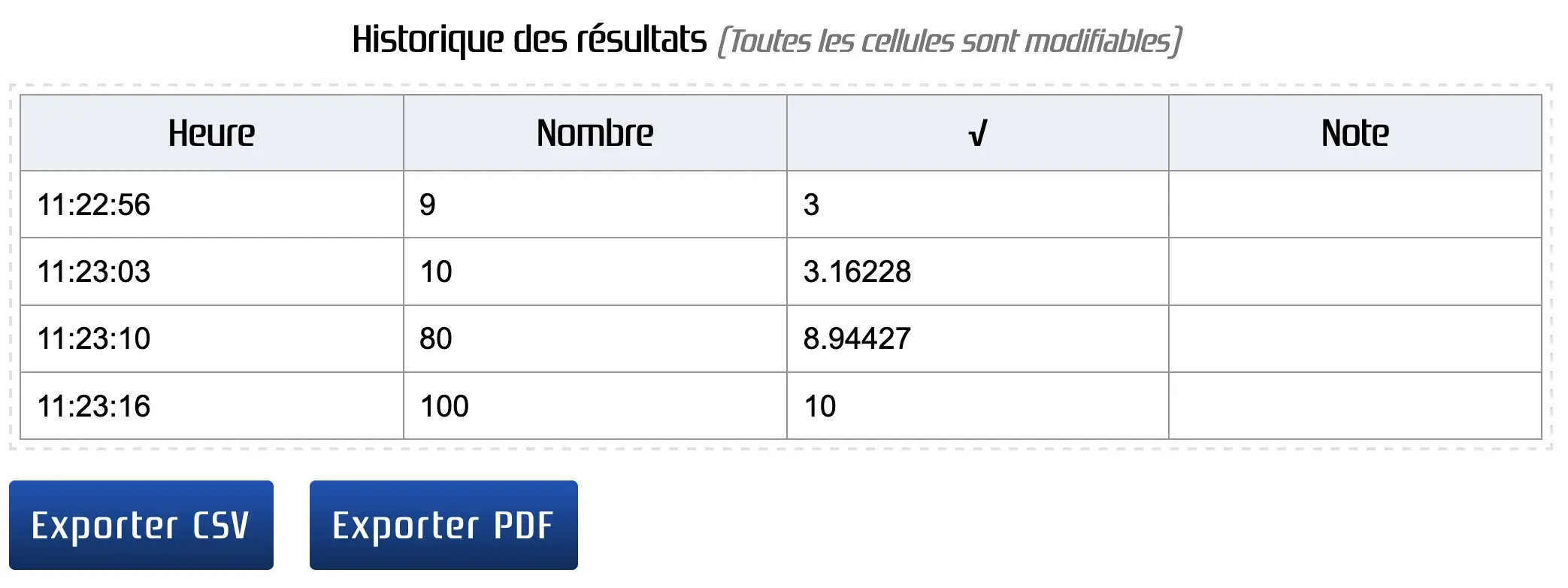
Sauvegarder les résultats

Pour conserver les résultats obtenus, appuyez sur le bouton Sauvegarde. Vos données seront alors enregistrées.

Exportation au format CSV

Vous pouvez exporter vos sauvegardes au format CSV, ce qui facilite l'importation dans des tableurs comme Microsoft Excel ou Google Sheets, pour une analyse plus approfondie.

Exportation au format PDF

Il est également possible d'exporter vos sauvegardes au format PDF. Cela permet de partager ou d'archiver facilement vos résultats.

Effacer toutes les données

Si vous souhaitez réinitialiser les données, utilisez le bouton RESET pour effacer toutes les données en une seule fois.

Importance de la racine carrée

La racine carrée est une opération mathématique importante utilisée dans de nombreux domaines comme les statistiques, la physique et l’ingénierie. Elle est nécessaire pour calculer des mesures comme l’écart-type, trouver des distances dans des espaces complexes, ou résoudre des équations du second degré. Comprendre la racine carrée aide à mieux analyser les données et à rendre les calculs plus précis.